1. Introduction
Transformer, 一种使用注意力(Attention)来加速训练的模型,这个模型最大的好处是可并行,即所有单词是同时训练的,这就大大增加了计算效率。Transformer使用了位置嵌入(Positional Encoding)来理解语言的顺序,使用自注意力机制(Self-Attention Mechanism)和全连接层进行计算。
2. Abstract Model
我们先将整个模型视为黑盒(Black Box),比如在机器翻译中,模型接收一种语言的句子作为输入,然后用另一种语言输出它的翻译。

进一步拆解,我们看到这个模型由编码层(Encoding)、解码层(Decoding)以及它们之间的连接层(Connection)组成。
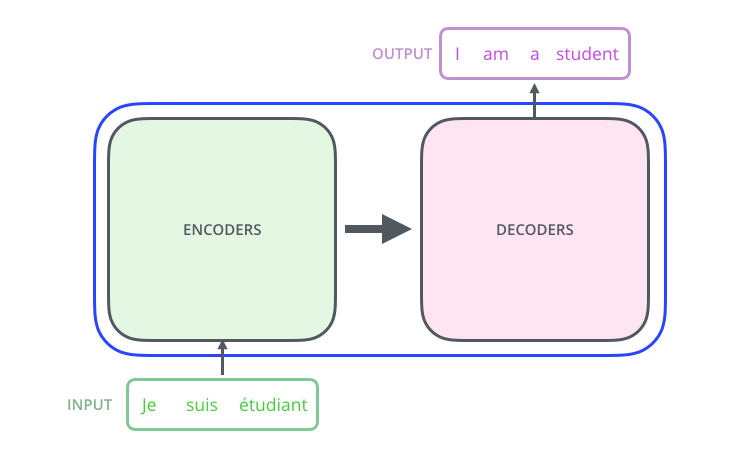
编码层由多个编码器(Encoder)构成,解码层也由数量相同的解码器(Decoder)构成。编码层负责把输入(语言序列)映射成隐藏层,然后解码层再把隐藏层映射成自然语言序列。下文中我们会进一步看到:解码层输出的时候,通过\(N\)个解码器才输出一个Token,并不是通过一个解码器就输出一个Token.
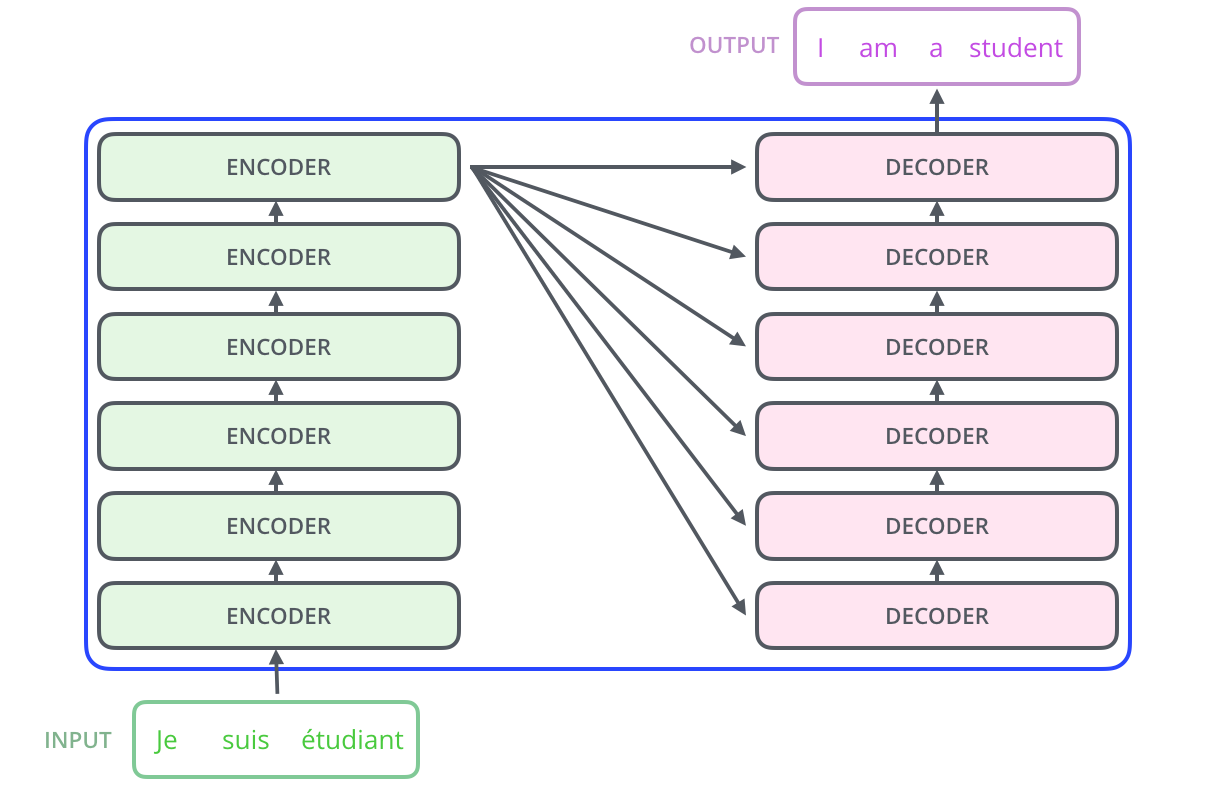
编码器在结构上都是相同的(但并不共享参数),每一个编码器都可以分为两个子层:
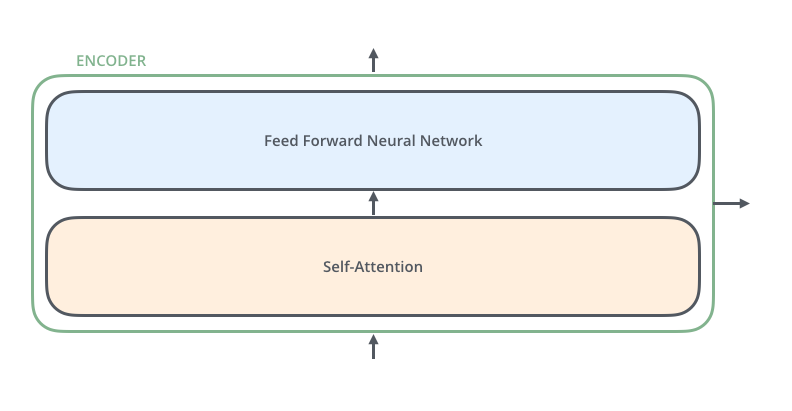
编码器的输入首先通过自注意力层——一个帮助编码器在编码特定单词时查看输入句子中其它单词的层。自注意力层的输出反馈给前馈神经网络(Feed-Forward Neural Network),每个输入位置对应的前馈神经网络是独立的。
解码器同样也有这两个子层,但在两个子层间增加了注意力层,帮助解码器关注输入句子的相关部分。
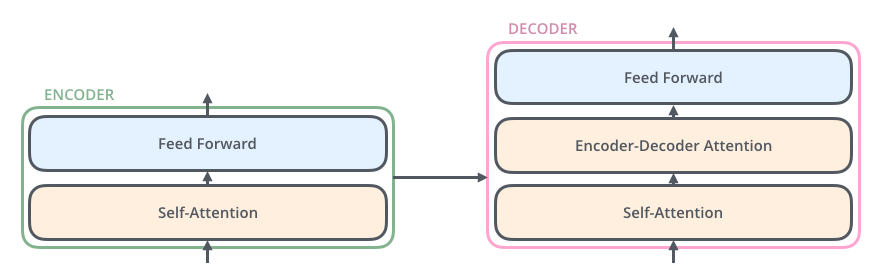
3. Encoding
正如自然语言处理(Natural Language Processing,NLP)应用的常见例子,我们首先使用嵌入(Embedding)算法将每个输入单词转换为向量(假设每个词映射到512维的向量上):

嵌入只会发生在最底层的编码器中。每个编码器都会接收一个由大小为512的向量组成的列——在底层编码器中是词嵌入,而在其它编码器中是前一个编码器的输出。列的大小是可以设置的超参数,通常这是训练集中最长句子的长度。
在输入序列的单词嵌入后,每个词嵌入都会通过编码器的两个子层。
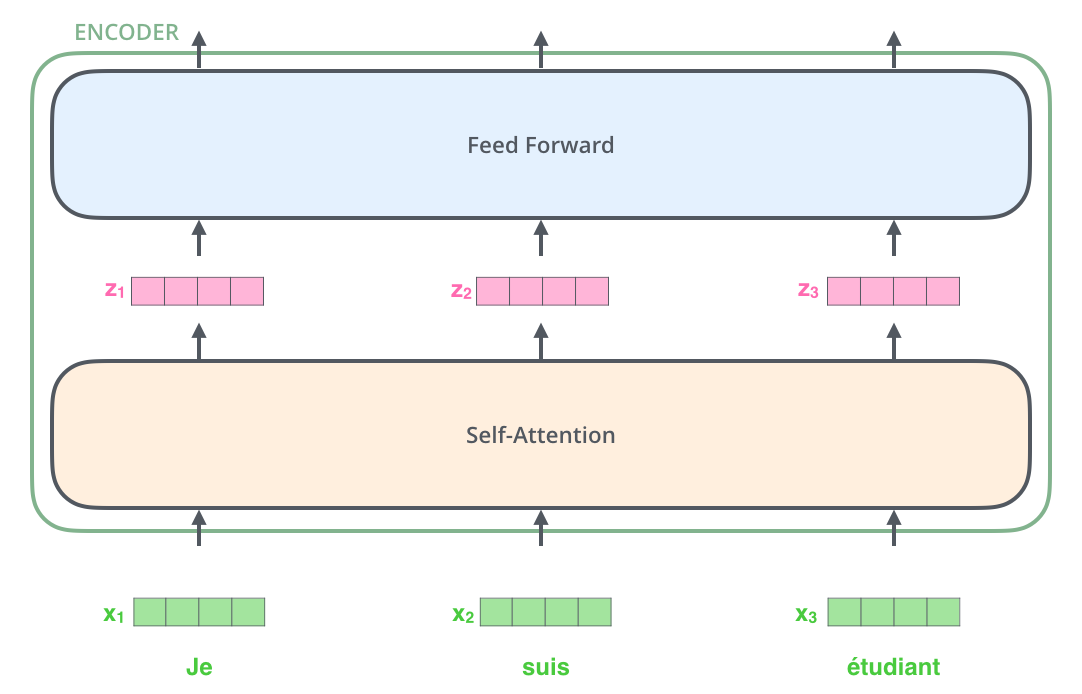
在这里,我们要注意到Transformer的一个重要性质,即每个位置的单词仅仅经过自己的编码器路径。在自注意力层中,这些路径是相互依赖的。然而,前馈层没有这些依赖关系,因此这些路径在经过前馈层时可以并行执行。
正如前文所提到的一样,编码器接收由向量组成的列作为输入,然后将其传入自注意力层处理,再传入前馈神经网络,最后将输入传入下一个编码器。
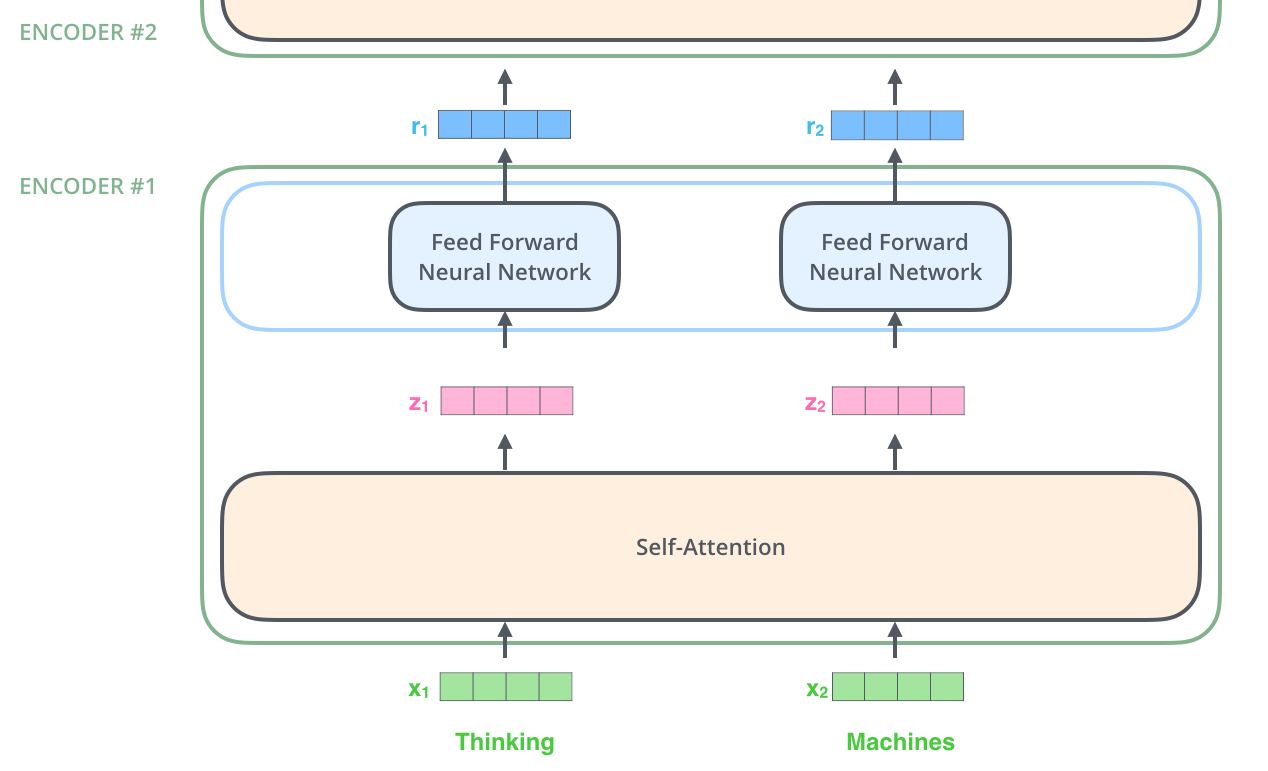
4. Self-Attention
4.1. Abstract Model
假设这一句话是要翻译的输入语句:The animal didn't cross the street because it was too tired. 这个句子中的it指的是什么?是指street还是指animal?对人类而言,这是一个简单的问题,但对算法来说却不简单。当模型处理单词it时,自注意力机制允许它将it和animal联系起来。
当模型处理每个单词(输入序列中的每个位置)时,自注意力允许它查看输入序列中的其它位置,以寻找有助于更好地编码该单词的线索。Transformer使用自注意力来将相关单词的理解编码到当前正在处理的单词中。
4.2. Self-Attention in Detail
我们先来看下如何用向量计算自注意力,再看下如何用矩阵计算。
第一步,根据编码器的输入向量,生成三个向量。比如,对每个单词,生成查询(Query)向量、键(Key)向量和值(Value)向量。这些向量是根据嵌入乘以在训练过程中训练的三个矩阵得到的。注意,这些新向量的维度小于嵌入向量:新向量的维度是64,而嵌入和编码器输入及输出向量的维度是512. 新向量的维度不一定需要更小,但这样一种结构选择可以使多头注意力(Multi-Headed Attention)的计算更稳定。比如在下图中,\(\mathbf{x}_1 \cdot W^Q=\mathbf{q}_1\).
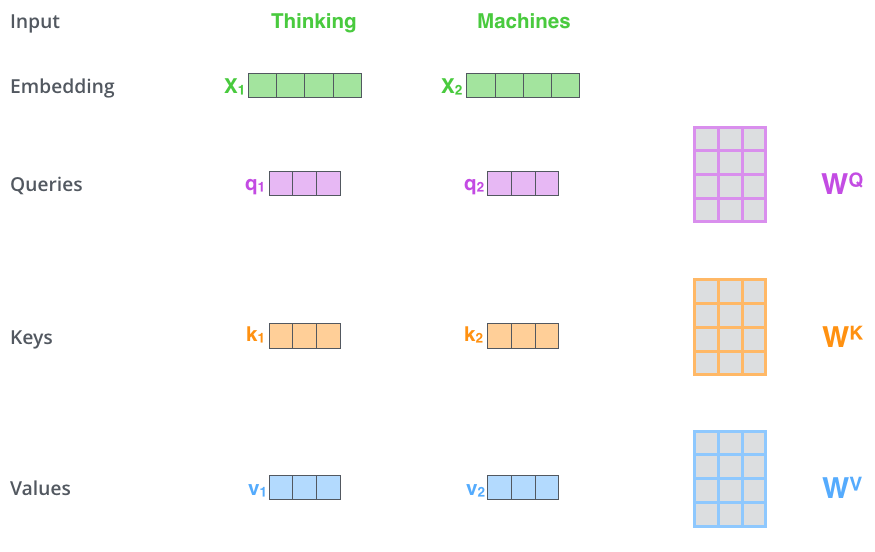
第二步,计算分值(Score)。假设我们计算上例中第一个单词Thinking的自注意力,我们需要给输入句子中的每个单词打分——分值决定了在某个位置对一个单词(比如Thinking)进行编码时,要把多少注意力放在输入句子的其它部分上。这个分值是通过查询向量(Thinking对应的查询向量)和所有单词的键向量依次做点积得到的。因此,当处理位置#1时,第一个分值是\(\mathbf{q}_1 \cdot \mathbf{k}_1\),第二个分值是\(\mathbf{q}_1 \cdot \mathbf{k}_2\).
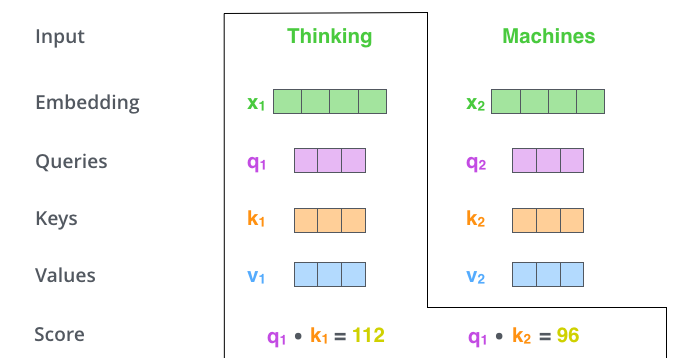
第三步和第四步是将分值除以\(\sqrt{\dim(\mathbf{k})}=8\), 这会使梯度更稳定。然后通过\(\text{softmax}\)传递结果——\(\text{softmax}\)将分值标准化,使其全部为正值且和为\(1\).
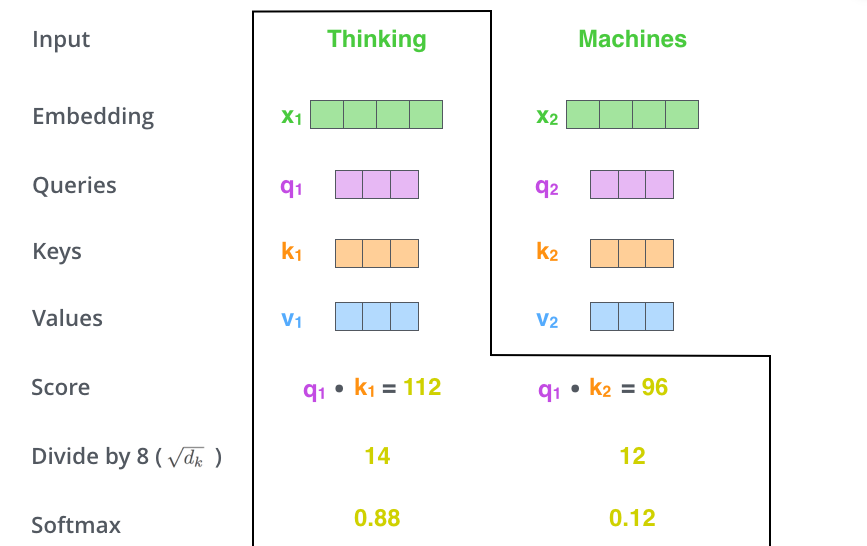
\(\text{softmax}\)分值决定着在这个位置,每个单词的表达程度(关注度)。很明显,这个位置上的单词将具有最高的\(\text{softmax}\)分值,但也有助于关注与当前单词相关的另一个单词。
第五步,将每个值向量与\(\text{softmax}\)分值相乘,保留想要关注的单词的值,并忽略不相关的单词。
第六步,对加权值向量求和,产生该位置的自注意力的输出结果。
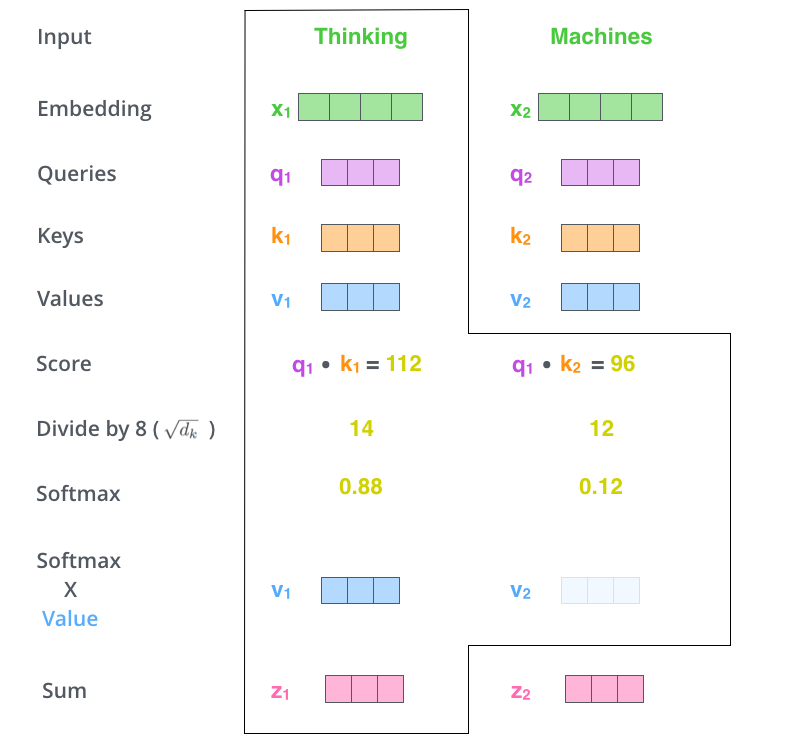
上述就是自注意力的计算过程,而生成的向量则继续传入前馈神经网络。在实际应用中,上述计算是以速度更快的矩阵形式进行的。
4.3. Matrix Calculation of Self-Attention
首先,计算查询矩阵、键矩阵和值矩阵。将所有词嵌入合并成输入矩阵\(X\)(\(X\)中第\(i\)行表示输入句子中的第\(i\)个单词的向量),并将其分别乘以训练的权重矩阵\((W^Q, W^K, W^V)\),得到\(Q\), \(K\)和\(V\)(矩阵中第\(i\)行表示第\(i\)个单词的查询/键/值向量)。
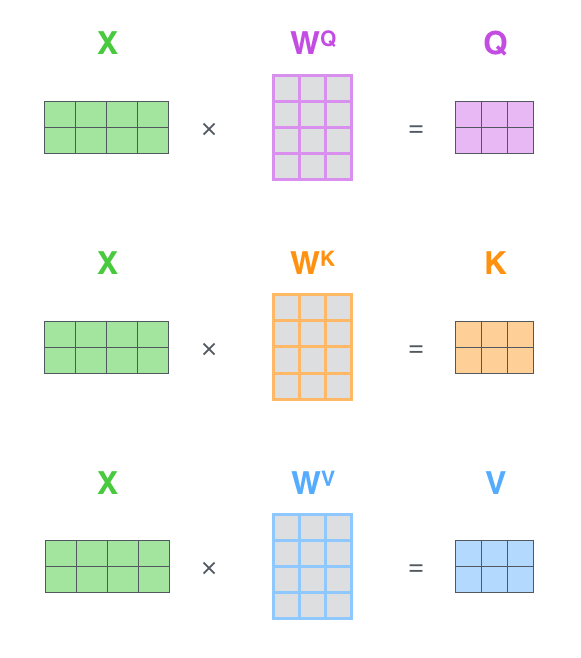
最后,由于我们使用矩阵处理,我们可以将上述步骤合并成一个计算自注意力层输出的公式。
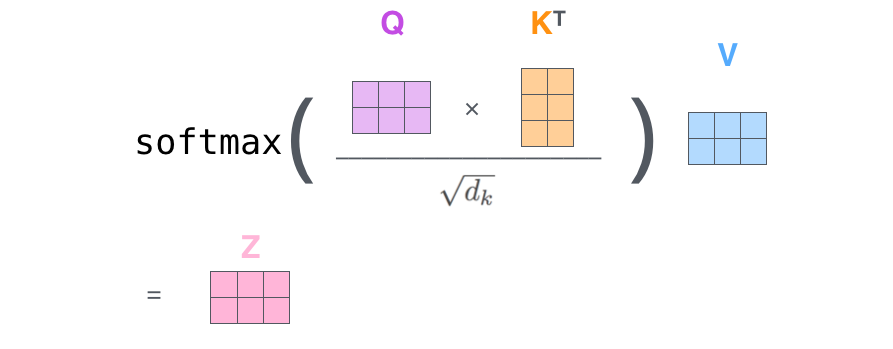
4.4. Multi-Headed Attention
我们通过增加多头注意力的机制,进一步细化了自注意力层,在如下两个方面提高了注意力层的性能:
- 多头注意力机制扩展了模型关注不同位置的能力。比如在上面的例子中,\(\mathbf{z}_1\)包含了一些其它的编码,但它可能还是被实际的单词本身所支配,而知道
it的指代对象对翻译The animal didn't cross the street because it was too tired会更有帮助。 - 多头注意力为注意力层提供了多个表示子空间(Representation Subspace)。像下面的例子所示,在多头注意力下有多组查询/键/值权重矩阵(Transformer使用八个注意力头(Attention Head),因此每个编码器/解码器有八组)。每一组都是随机初始化的,经过训练之后,输入向量可以被映射到不同的表示子空间中。
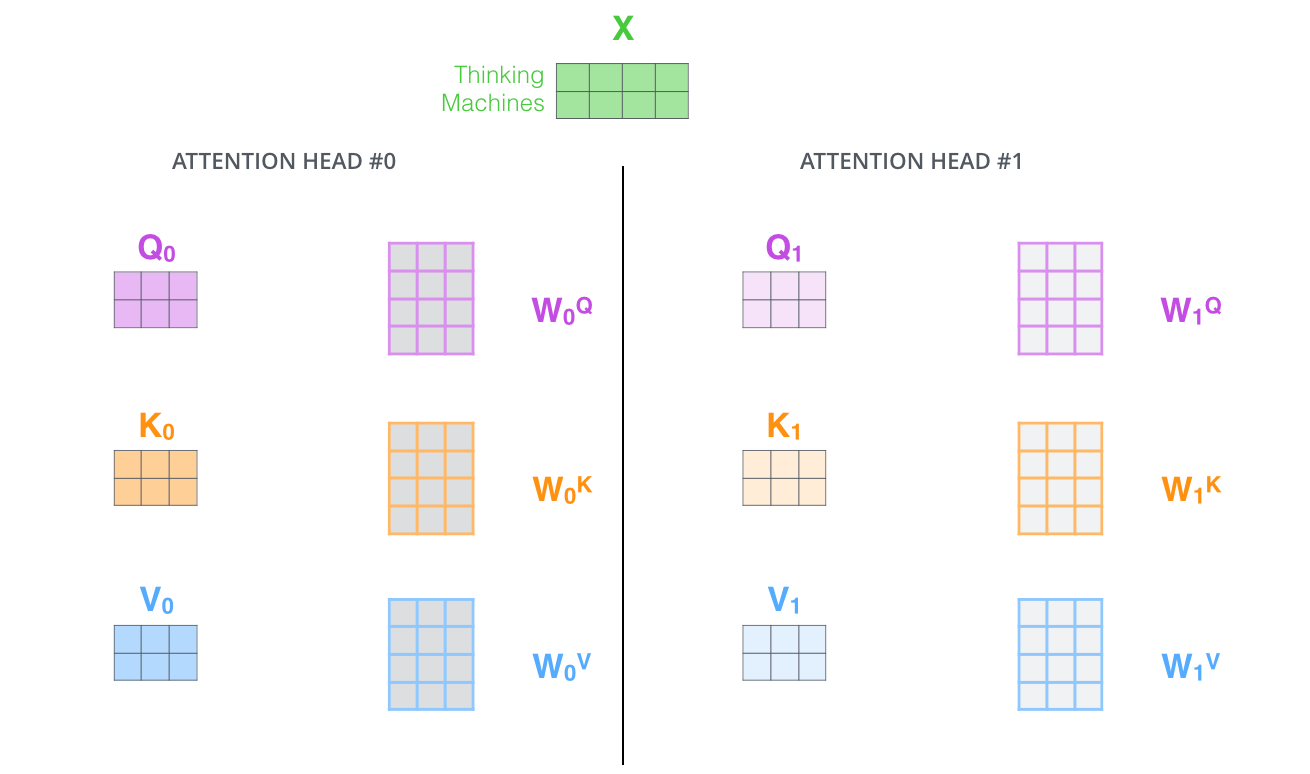
如果我们计算多头注意力的自注意力,只需要使用不同的权重矩阵进行八次不同的计算,最终得到八个不同的\(Z\)矩阵。
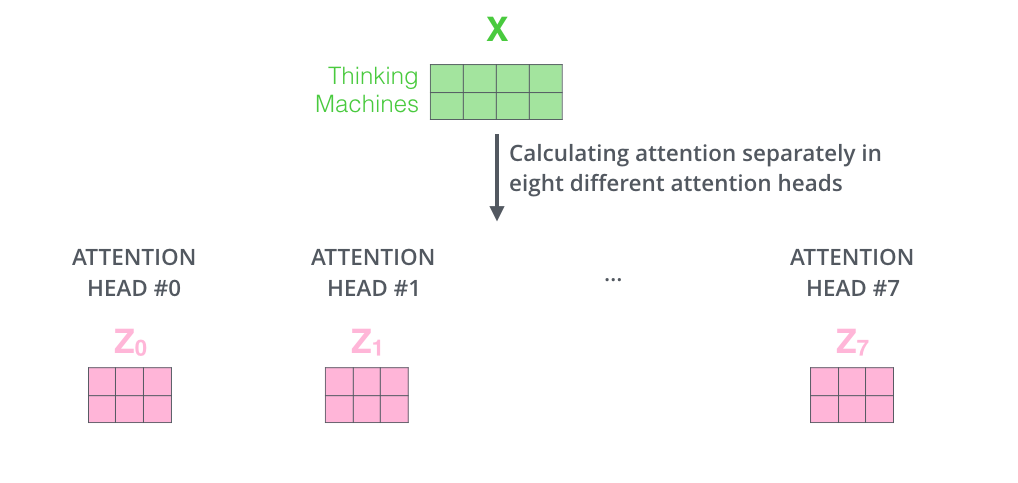
但这会带来一些麻烦:前馈层不能接收八个矩阵,所以我们需要一种方法将八个矩阵合并成一个矩阵——将矩阵合并,然后将这个大矩阵乘以一个额外的权重矩阵\(W^O\).
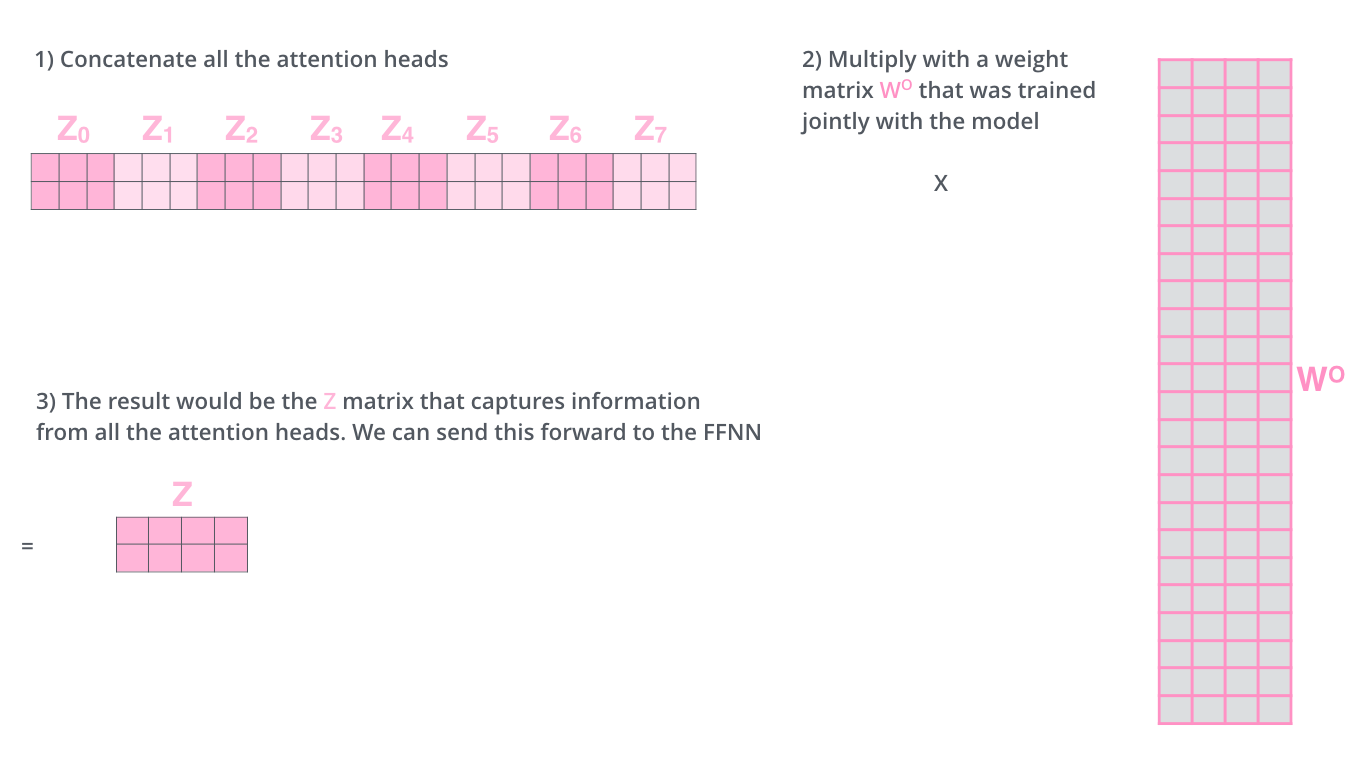
下面我们用一张完整图来表示多头注意力的自注意力。
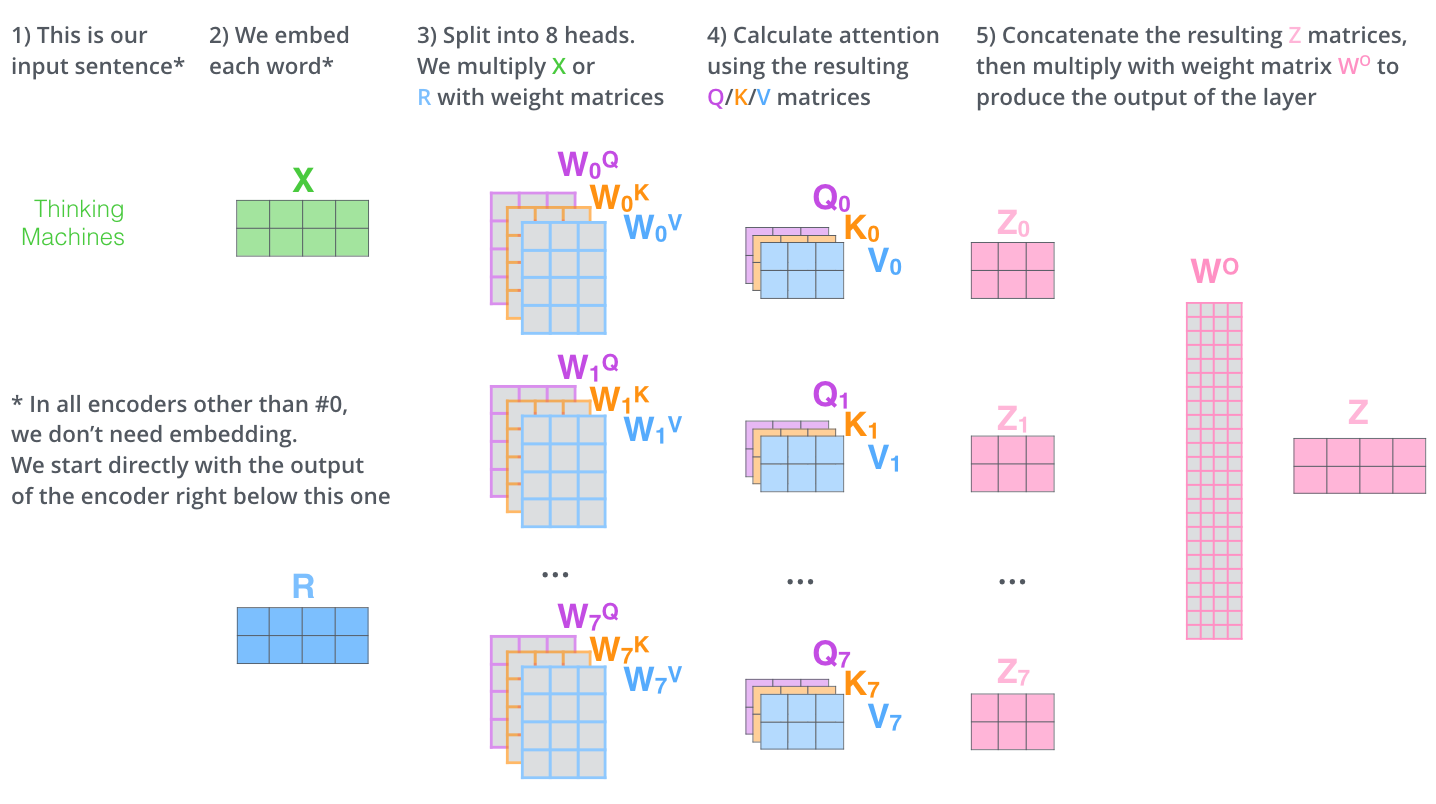
5. Positional Encoding
我们还没有讨论如何解释输入语句中单词的顺序——由于Transformer没有循环神经网络的迭代操作,所以我们必须提供每个单词的位置信息。
为了解决词序问题,我们定义位置编码(Positional Encoding),其形状为(max_seq_length, embedding_dim). 位置编码的维度与词嵌入的维度是相同的,均为embedding_dim; 而max_seq_length是超参数,指限定每个句子最长由多少个单词构成。
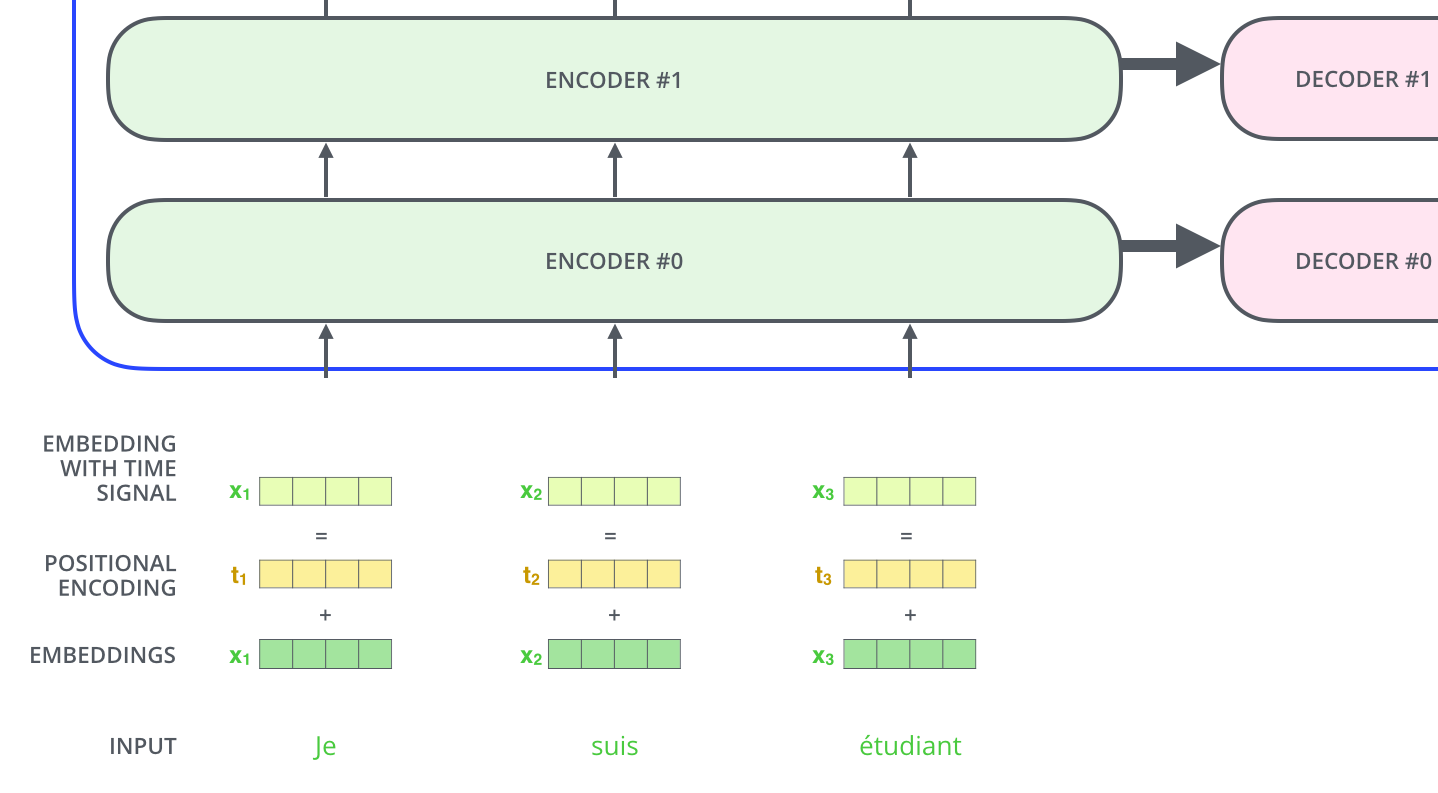
我们一般以单词为单位训练Transformer. 首先初始化单词编码大小(vocab_size, embedding_dim), 其中vocab_size为词库中所有词的数量,embedding_dim为词嵌入的维度。在PyTorch中是nn.Embedding(vocab_size, embedding_dim).
假设词嵌入(位置编码)的维度为4:
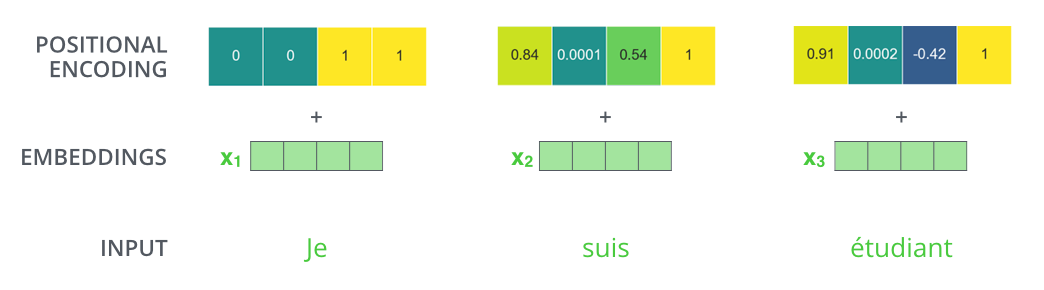
利用位置编码的公式可以生成相应的位置编码:\[\begin{aligned}
\text{PE}(\text{pos}, 2i)&=\sin(\text{pos}/10000^{2i/d_\text{model}}) \\
\text{PE}(\text{pos}, 2i+1)&=\cos(\text{pos}/10000^{2i/d_\text{model}})
\end{aligned}\] 其中\(\text{pos}\)指的是一句话中某个单词的位置,取值范围是\([0, \text{max_seq_length})\), \(i\)指的是词嵌入的维度序号,取值范围是\([0, \text{embedding_dim}/2)\), 以及\(d_\text{model}\)指的是embedding_dim的值。这不是位置编码的唯一方法,然而它的优点是能够处理未知长度的序列。
在下图中,每行对应一个向量的位置编码,比如第一行是我们在输入序列中嵌入第一个单词的向量。每行包含512个值,每个值范围在\([-1, 1]\).
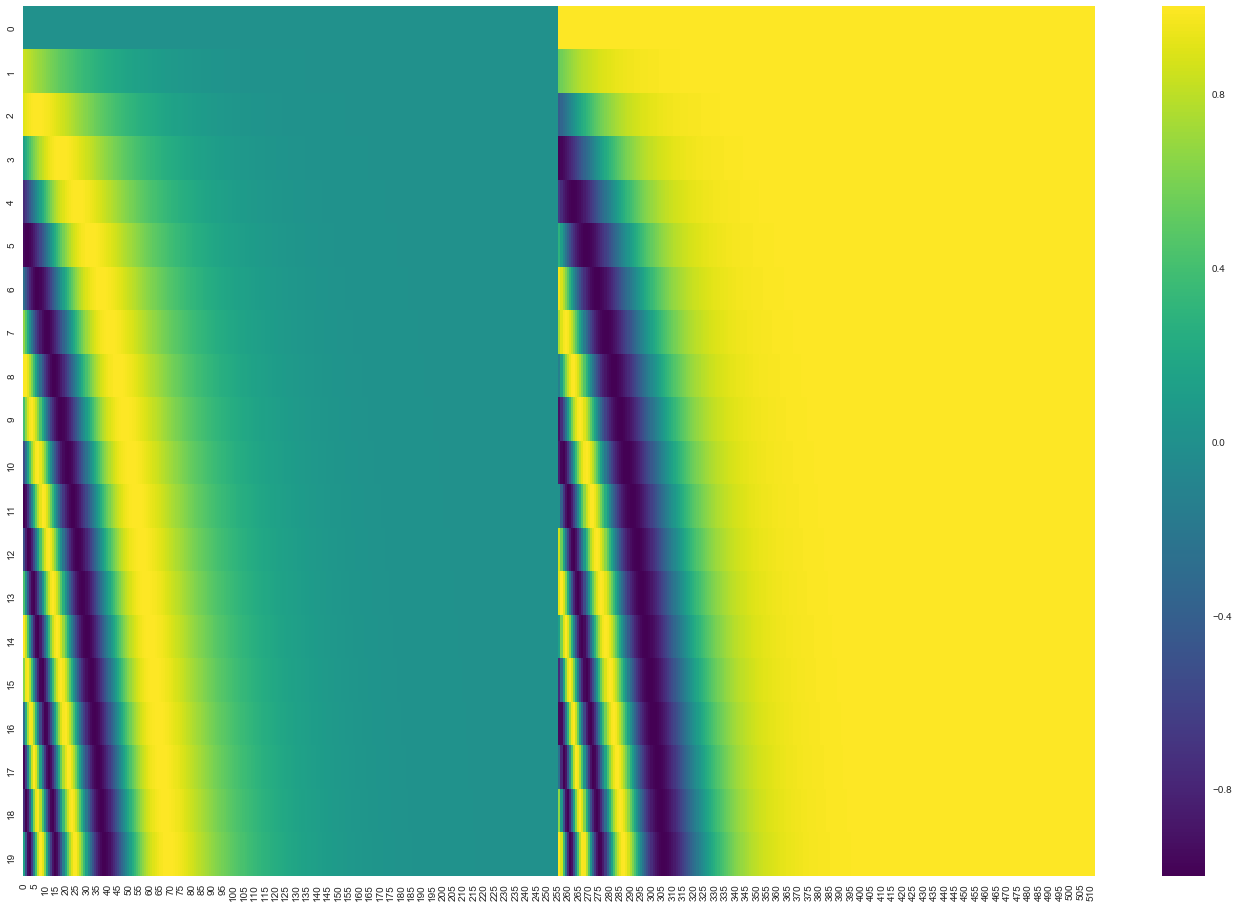
随着\(i\)增大(从左往右纵向观察),位置编码函数周期变化越来越平缓。
在Transformer中,位置编码是不可训练的,而在BERT中是可训练的。
6. Residual
编码器结构中值得注意的一个细节是,每个编码器中的每个子层都有残差(Residual)连接,并且紧跟着Layer-Normalization操作。
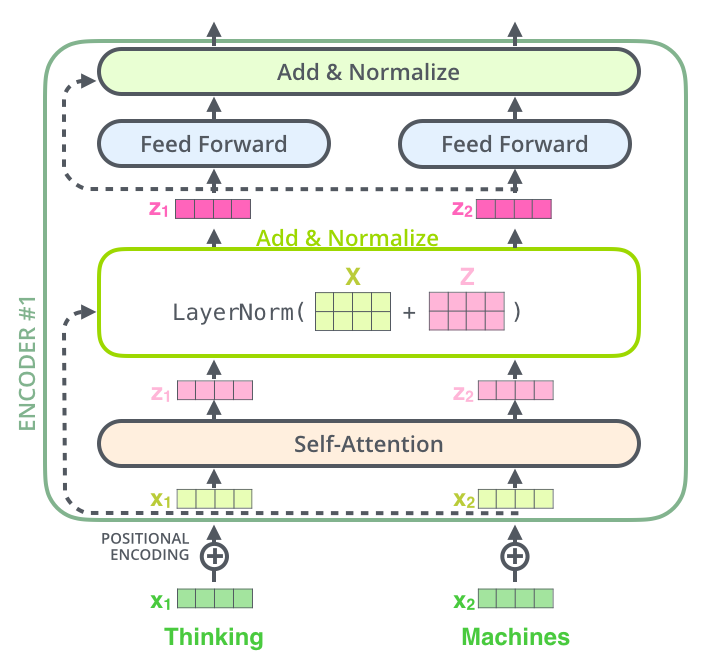
在解码器中也是如此,考虑由两层编码器和两层解码器组成的Transformer, 其结构如下:
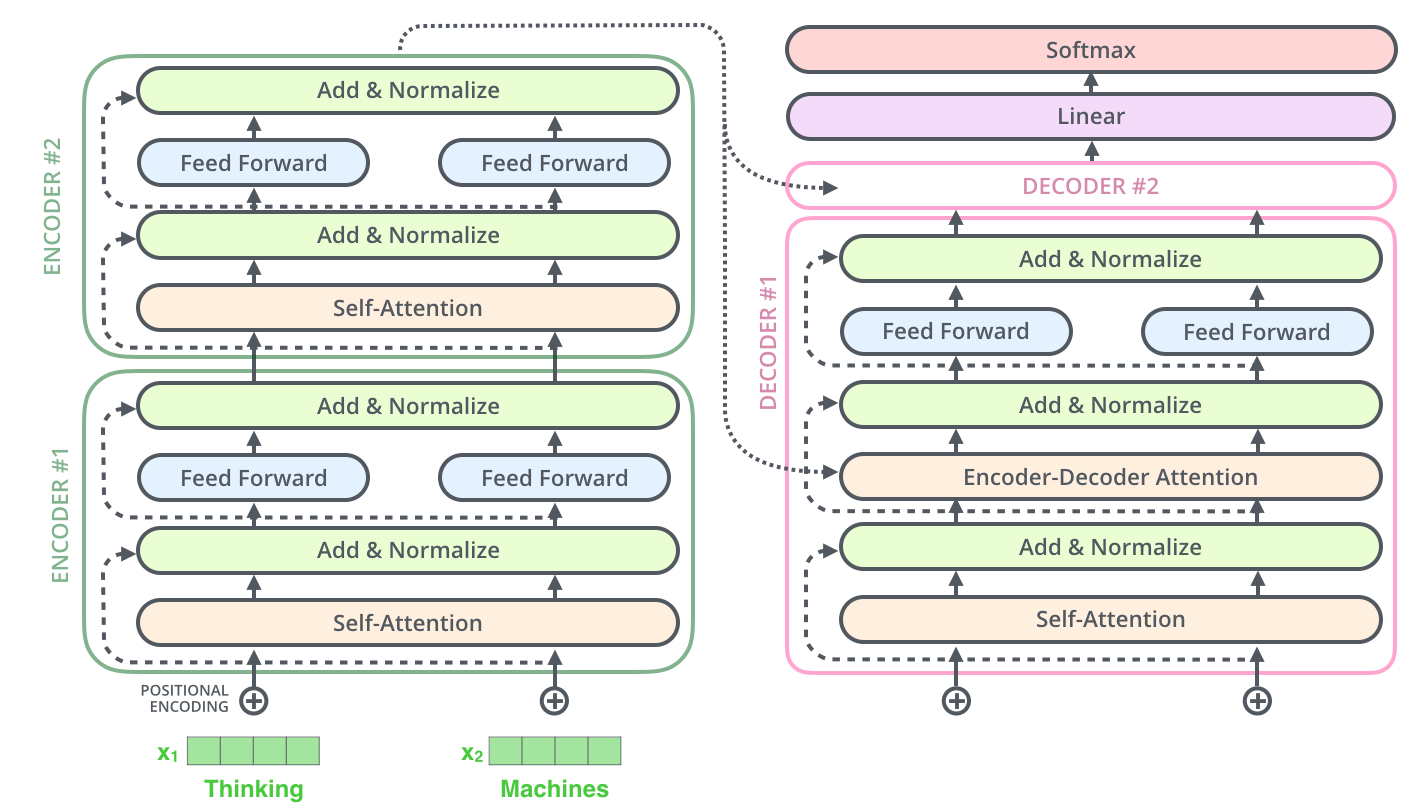
7. Encoder and Decoder
解码器和编码器的原理是类似的,现在我们来看看它们是如何协同工作的。
编码器从输入序列的处理开始,将顶部编码器的输出转换为一组注意力向量\(\mathbf{k}\)和\(\mathbf{v}\). 每个解码器将在其Encoder-Decoder Attention层中使用这些注意力向量,这有助于解码器集中在输入序列中的适当位置:
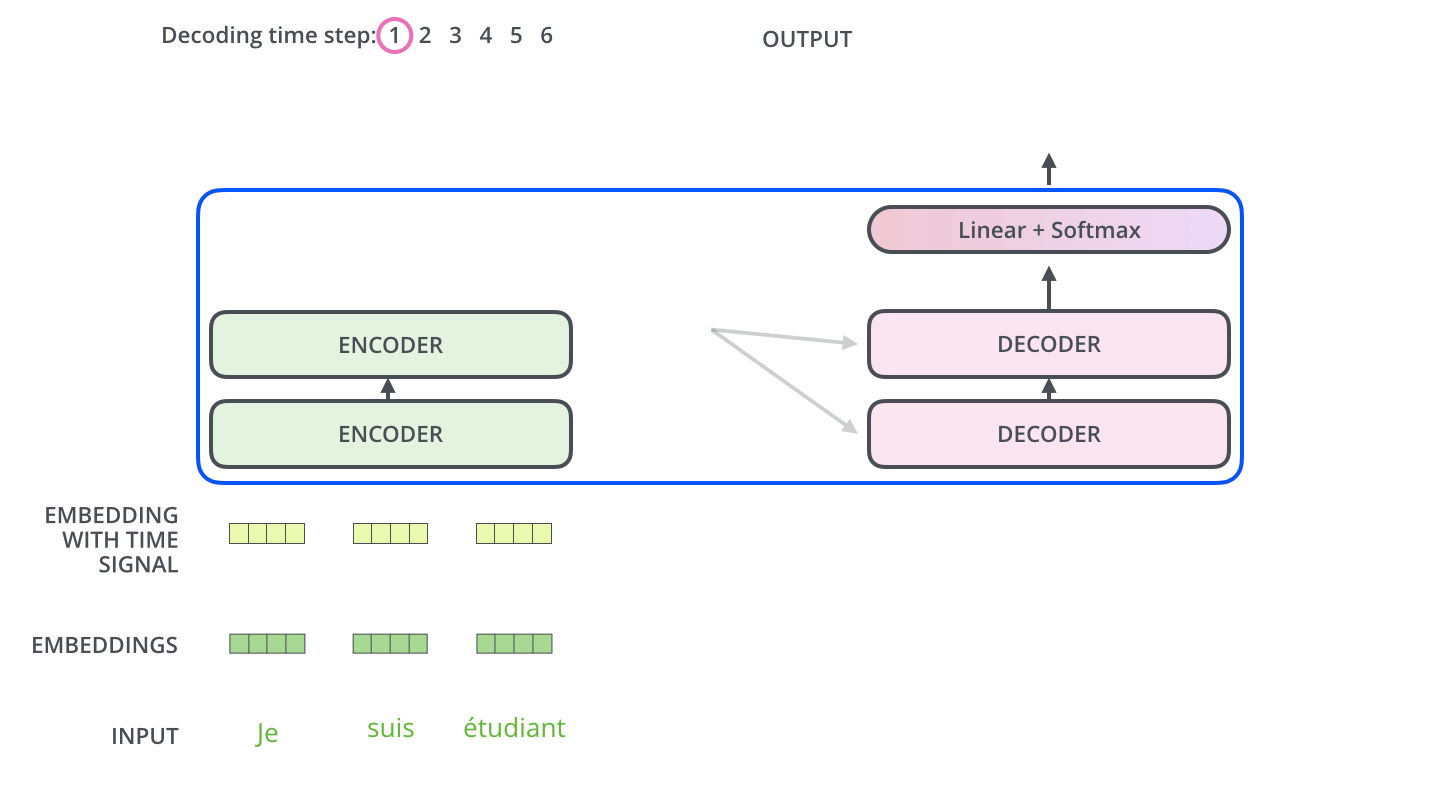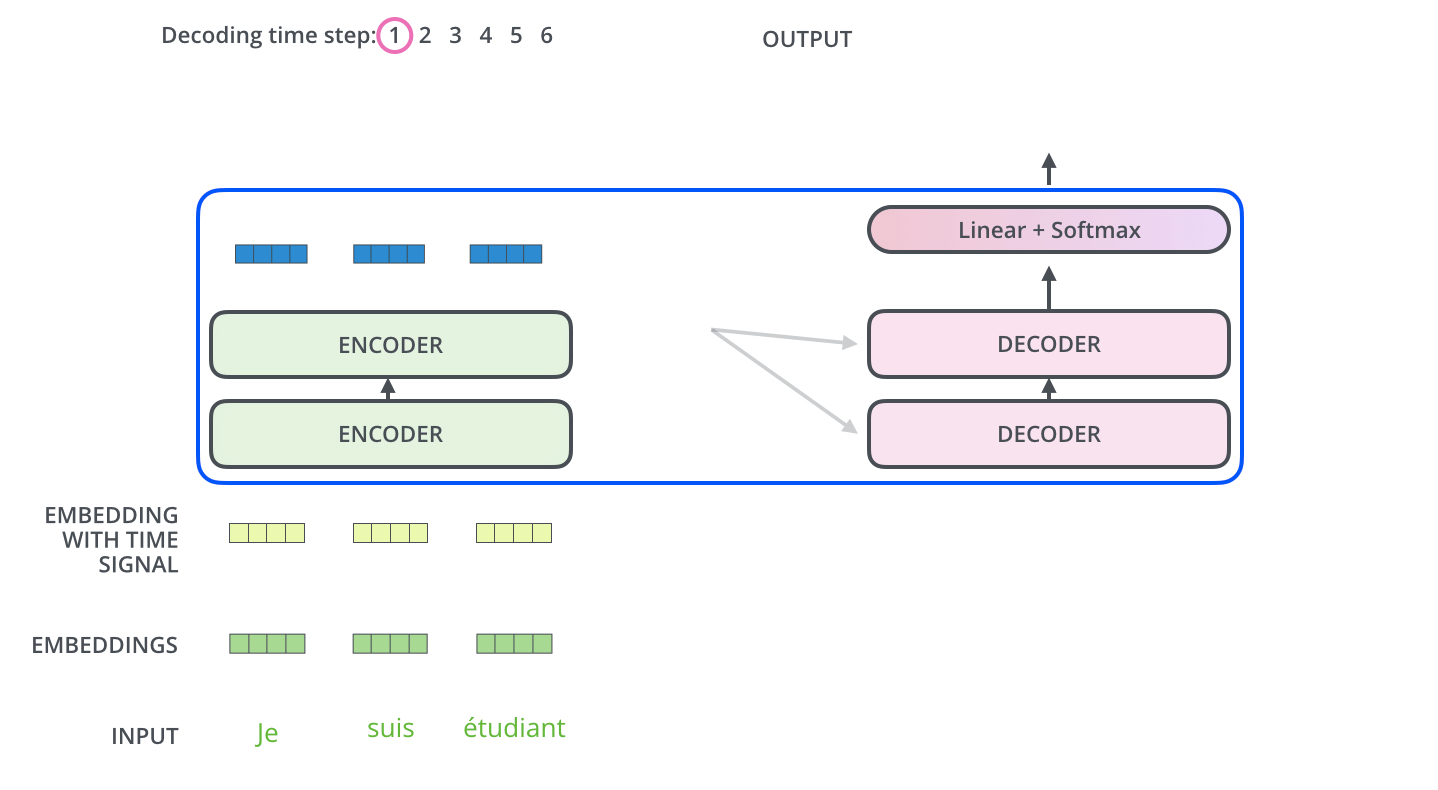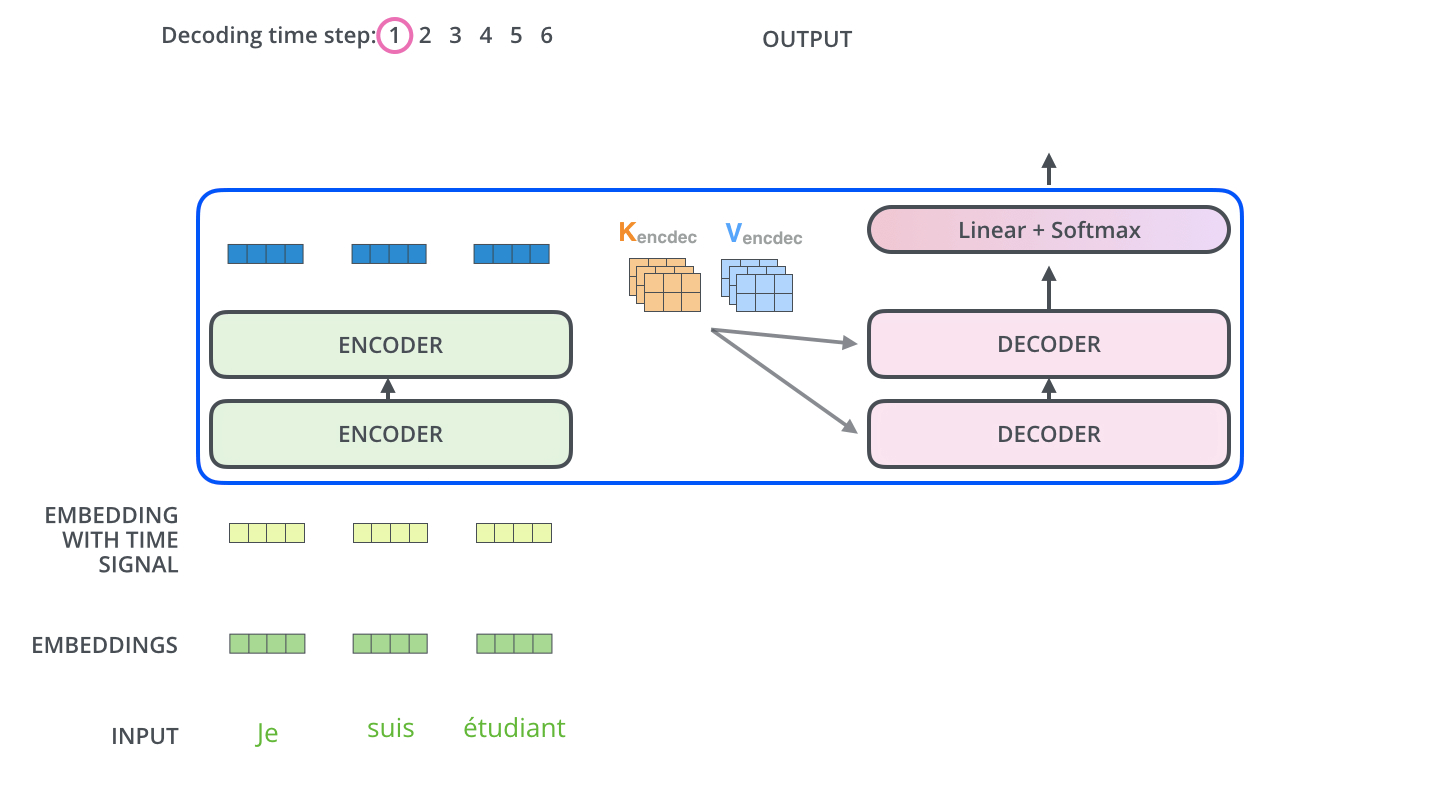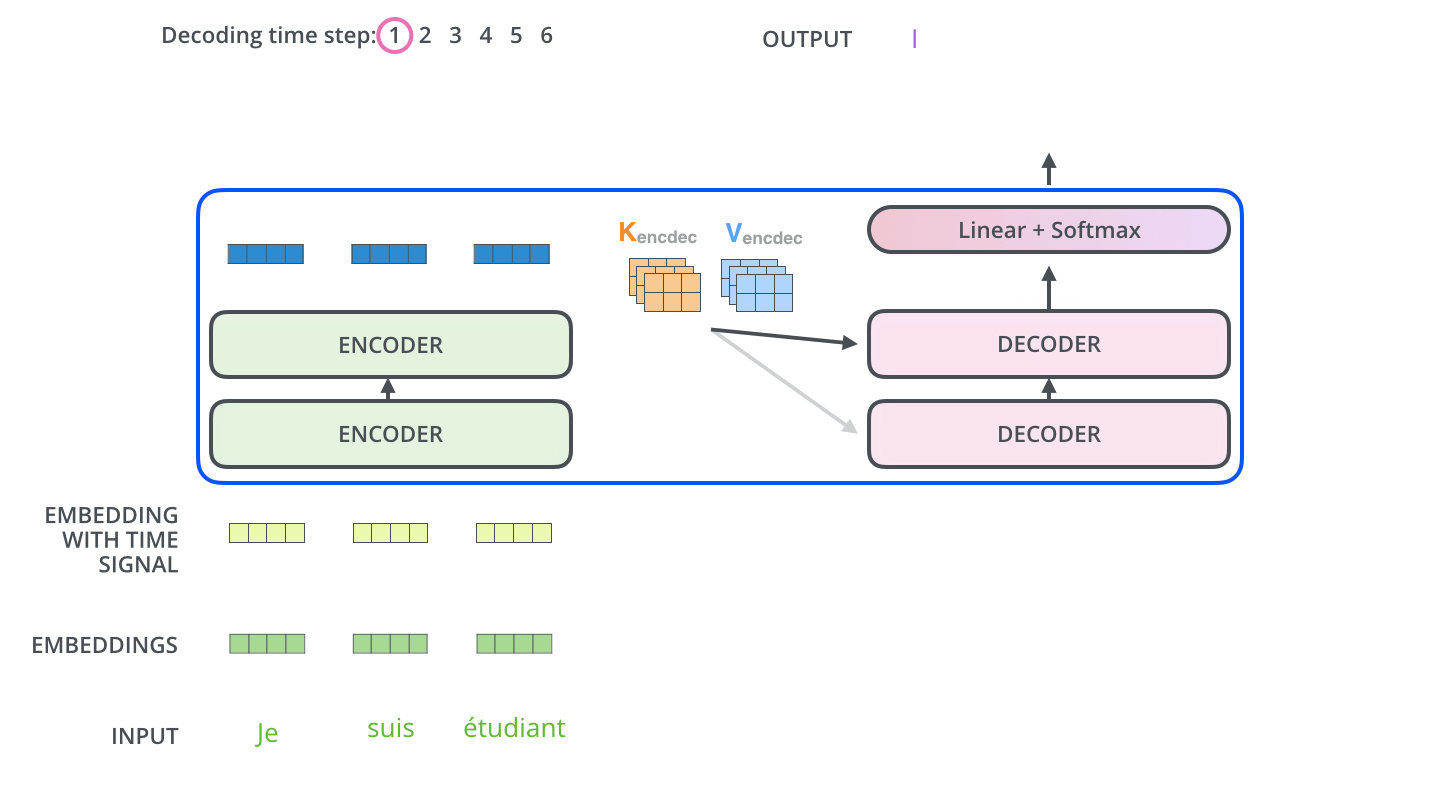
以下步骤一直重复,直到一个特殊符号出现指示Transformer解码器完成了翻译输出。每一步的输出在下一个时间步被馈送到底部解码器,解码器像编码器一样将其解码结果显示出来。此外,正如编码器的输入所做的处理,我们将位置编码嵌入并添加到解码器输入中,以指示每个单词的位置。
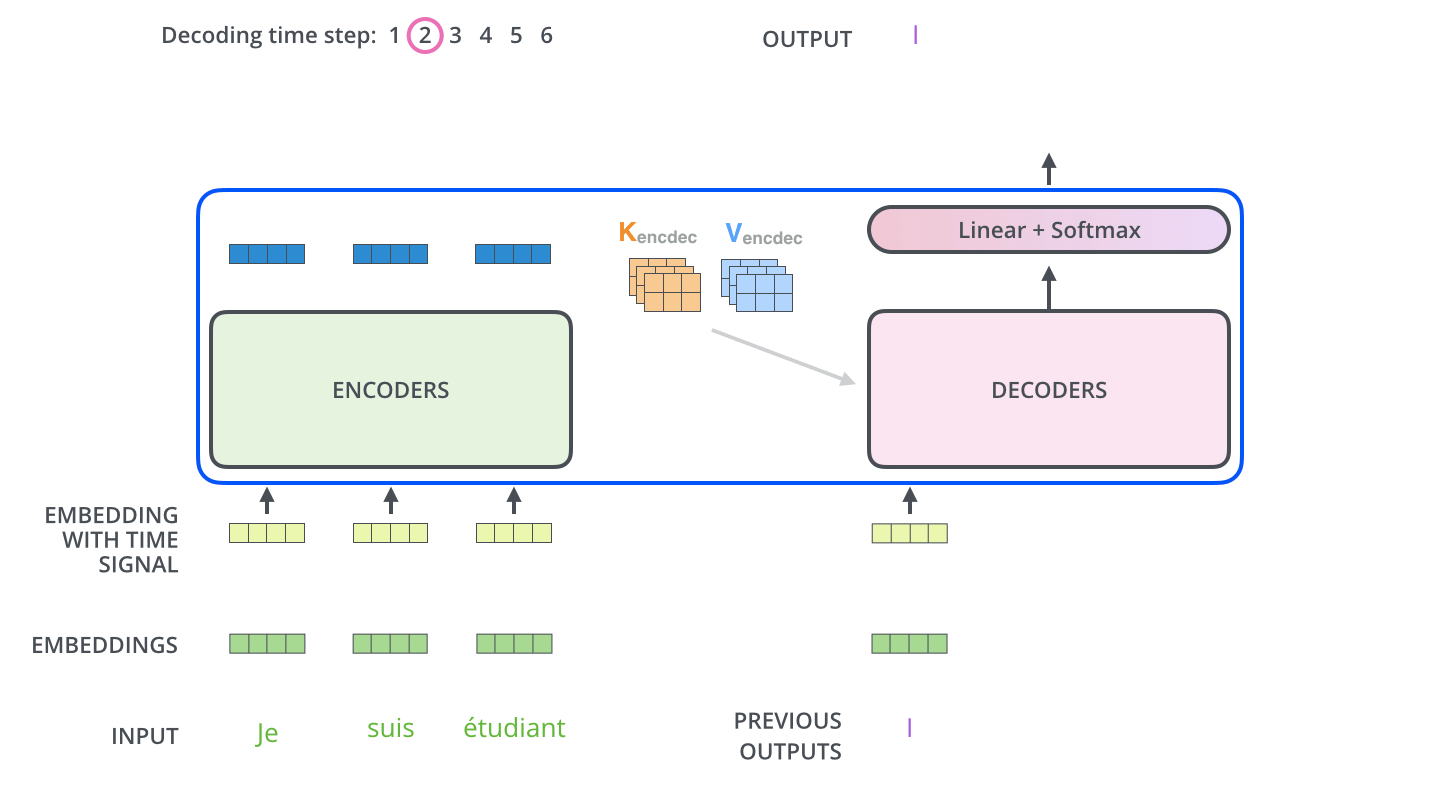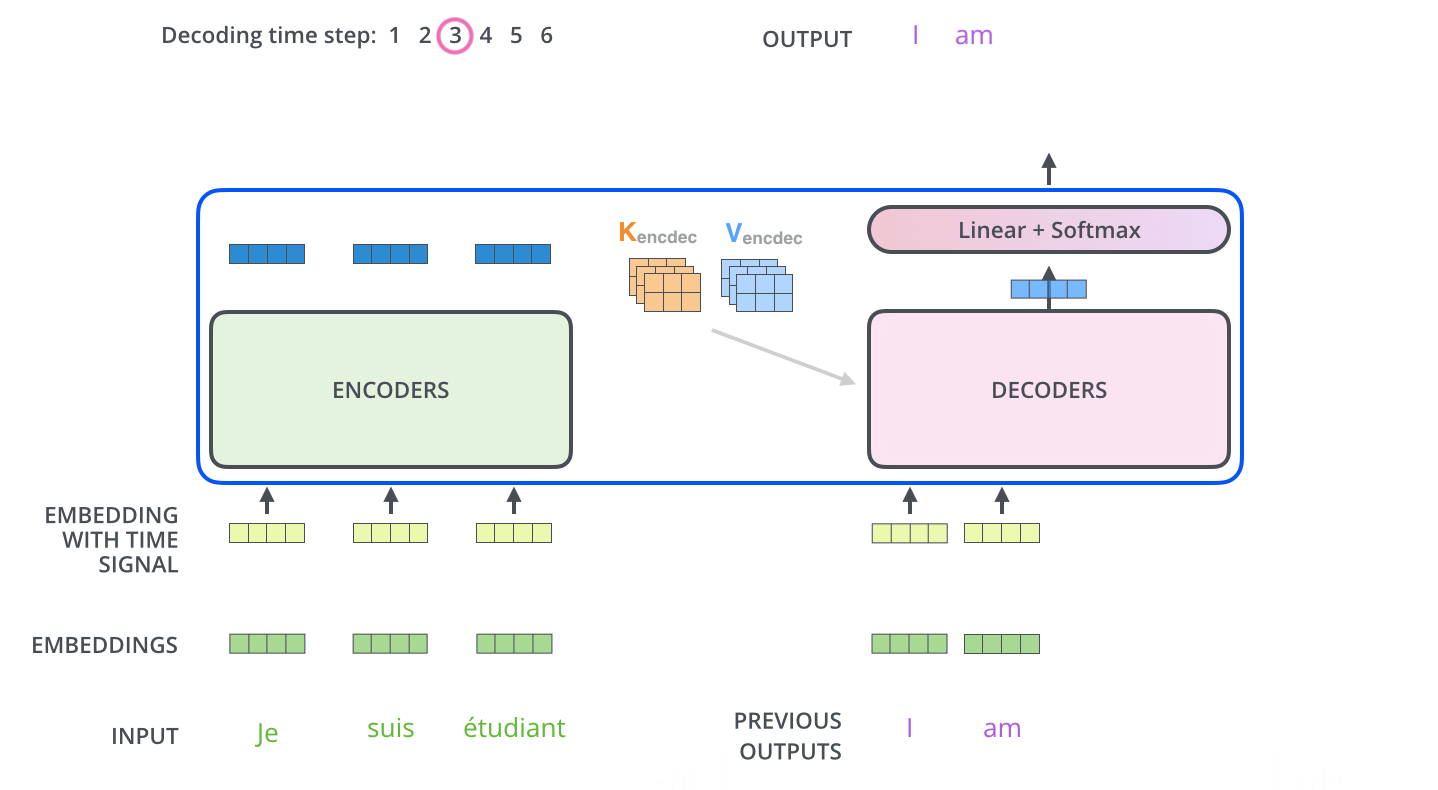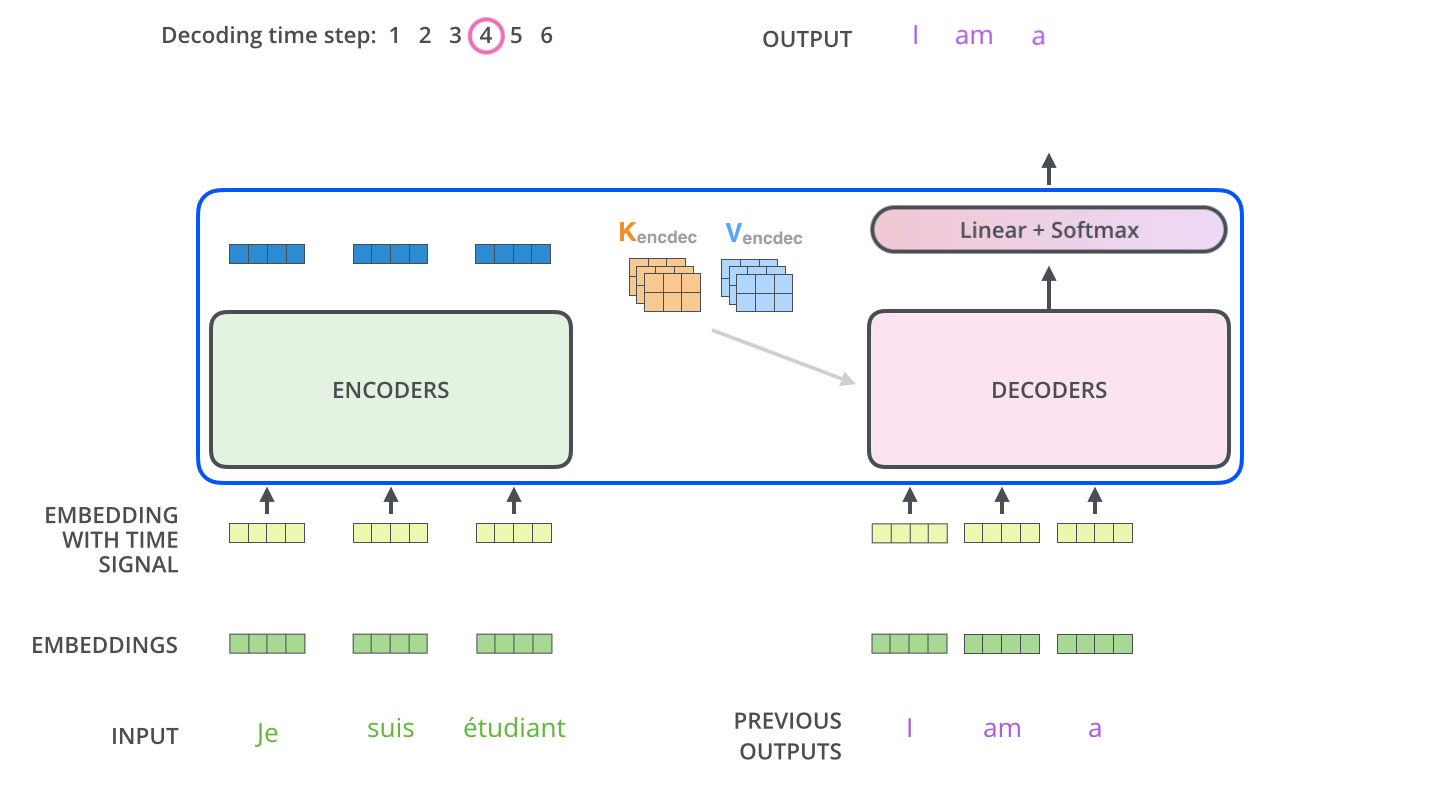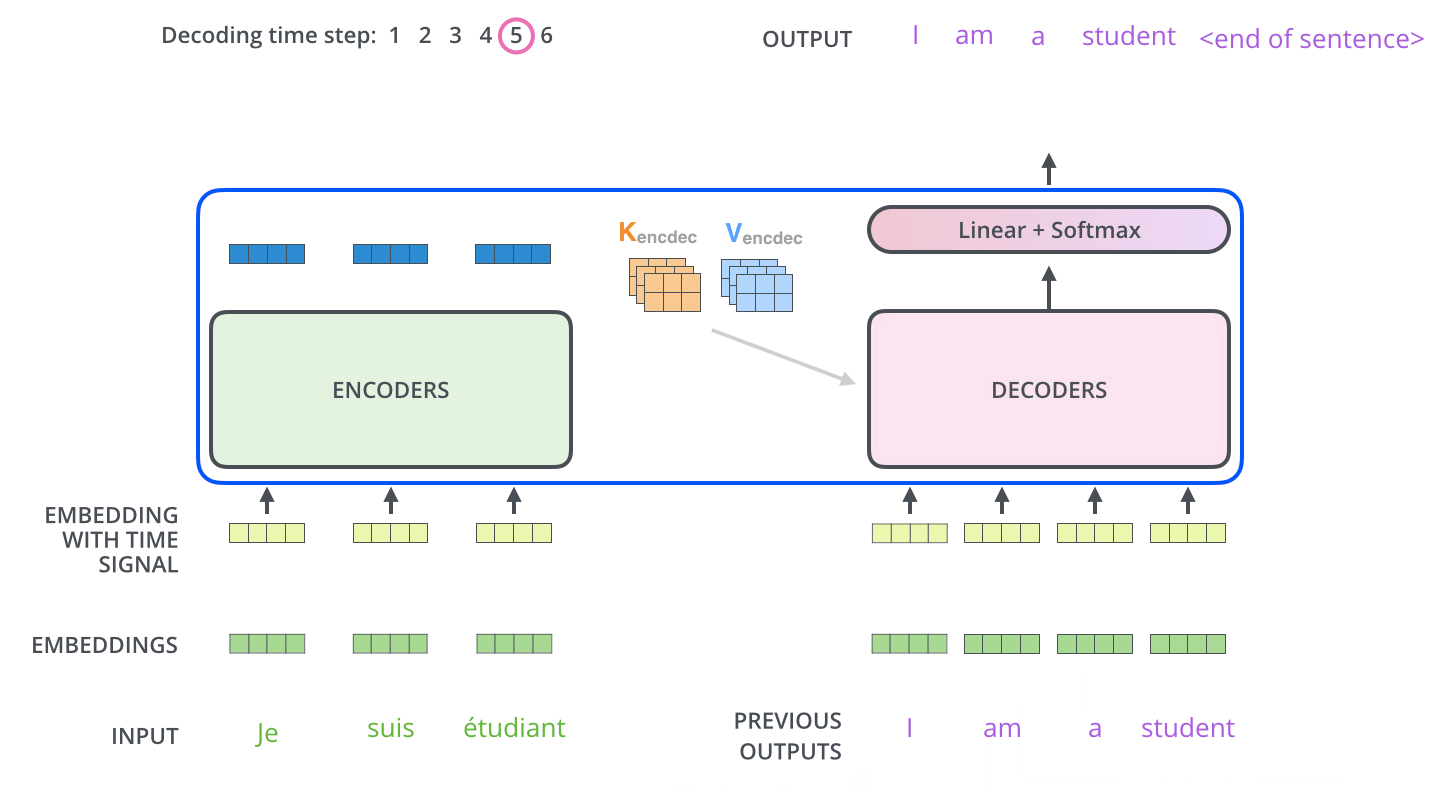
解码器中的自注意力层与编码器中的稍有不同:在解码器中,自注意力层只允许关注早于当前输出的位置——在\(\text{softmax}\)之前,通过遮挡未来位置(将其设置为-inf)来实现。
Encoder-Decoder Attention层的工作原理与Multi-Headed Self-Attention是类似的,只是它从下层创建Query矩阵,并从编码器的输出中获取Key矩阵和Value矩阵。
8. Linear and Softmax Layer
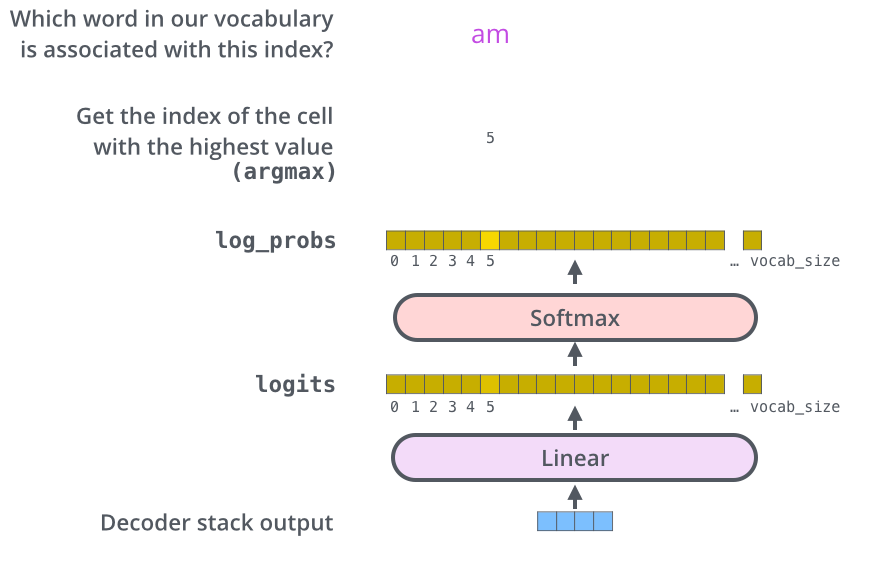
解码器输出浮点向量,而线性层和\(\text{softmax}\)层的主要工作是将其转化成单词。
线性层是一个简单的全连接层,它将解码器生成的向量映射到一个更大的向量,称之为logits向量。假设模型从训练集中学习了10000个单词(输出词表),那么logits向量为10000维,每个分量表示某个单词的分值。然后\(\text{softmax}\)层将这些分值转换为概率(全为正值且和为\(1\)),最高值对应的分量上的单词就是这一步的输出单词。
9. Loss Function
我们用一个简单的例子来示范训练,比如将merci翻译为thanks, 这意味着输出的概率分布指向单词thanks. 但由于模型未经过训练,所以不太可能就是期望的输出。由于模型的参数都是随机初始化的,未训练的模型输出随机值,而我们可以对比实际输出,然后利用反向传播调整所有模型的参数,使输出更接近实际输出。
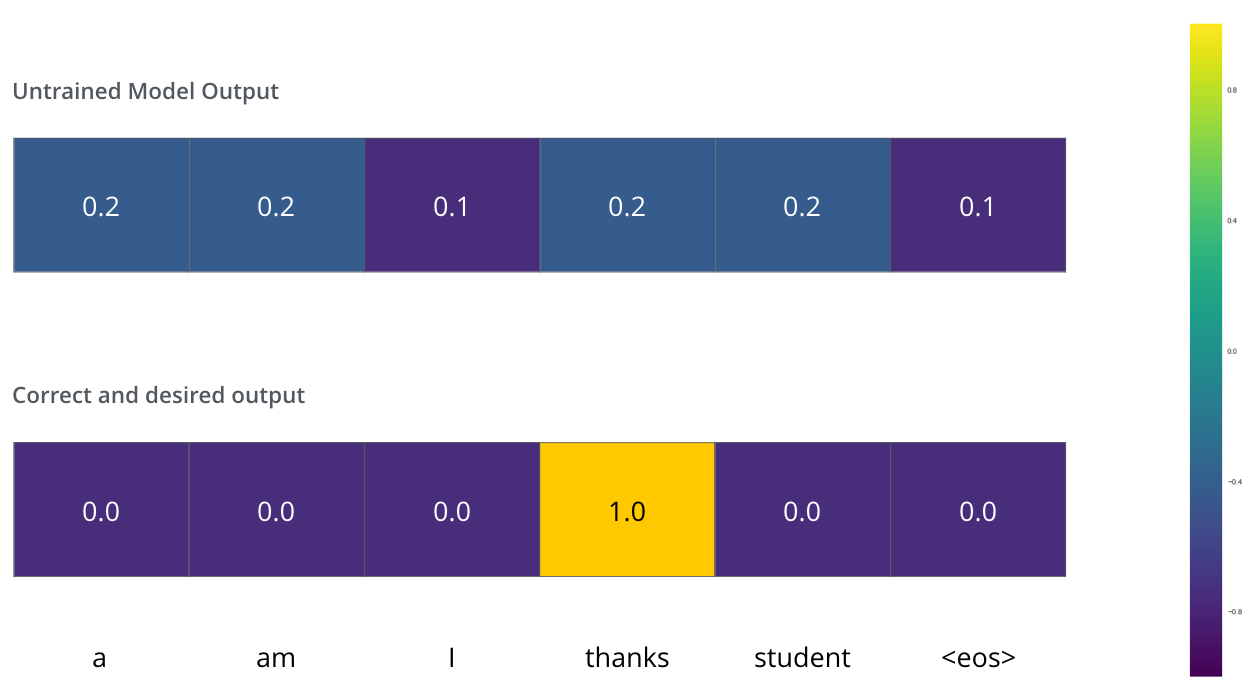
我们可以简单采用交叉熵(Cross Entropy)或Kullback-Leibler散度(KL Divergence)对比两个概率分布。
这是一个过于简单的例子,而更真实的情况是,使用一个句子作为输入,比如输入Je suis étudiant., 期望输出是I am a student. 在这个例子下,我们期望模型连续输出概率分布并满足以下条件:
- 每个概率分布由一个宽度为
vocab_size的向量表示(一般而言为30000或50000); - 第一个概率分布对
I具有最高的概率; - 第二个概率分布对
am具有最高的概率; - 依此类推,直到第五个输出分布指向
<end of sentence>符号。
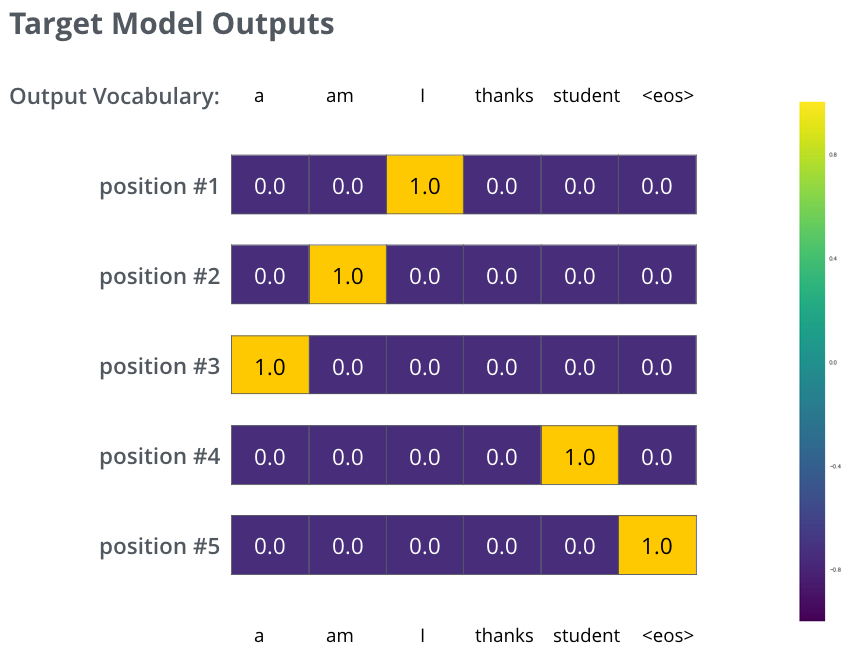
在足够大的训练集上训练足够时间后,我们希望生成的概率分布如下所示:
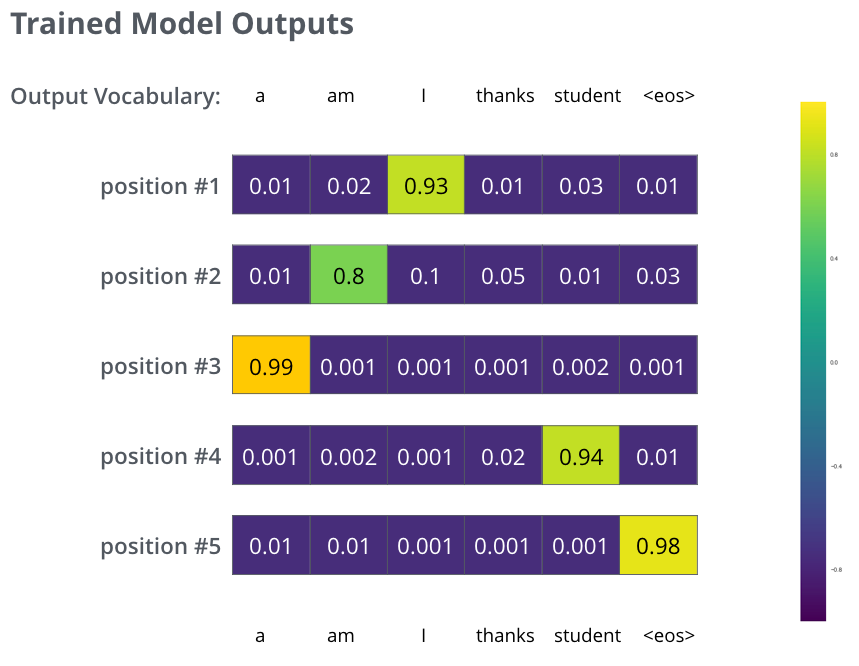
由于模型一次生成一个输出,我们可以假设模型从概率分布中选择概率最高的单词,然后丢弃其余单词,这种方法称为贪婪解码(Greedy Decoding)。另一种方法是波束搜索(Beam Search),比如说我们保留概率最高的两个单词(假设是I和a),在下一步运行模型两次:一次假设第一个输出位置是I,另一次假设第一个输出位置是a,同时考虑位置#1和#2,产生误差较小的模型被保留,然后我们对每一个位置重复这一操作。在我们的例子中,beam_size=2(意味着在任何时候,内存都保留两个部分的假设——未完成的翻译)以及top_beams=2(意味着模型将返回两次翻译)——这些都是我们可以在实践中调整的超参数。